- 时间复杂性
- 常数阶 O(1)
- 线性阶 O(n)
- 对数阶 O(logN)
- 平方阶 O(n2)
- 数据结构
- 链表
- 数组
- 栈
- 队列
- 堆
- 树
- 图
- 布隆过滤器
- LRU Cache
- 散列表
- 并查集
- 算法
- 排序算法
- 递归
- 哈希算法
- 二分查找
- 搜索算法
- 字符串算法
- 1. 五大算法
- 贪心算法
- 分治算法
- 位运算
- 回溯算法
- 动态规划
- 实例
- 两数之和
- 数据树
- 天平找次品
- TopK 问题
时间复杂性
在计算机科学中,时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大 O 符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。
常见的时间复杂度量级有:
- 常数阶 O(1)
- 线性阶 O(n)
- 对数阶 O(logN)
- 线性对数阶 O(nlogN)
- 平方阶 O(n2)
- K 次方阶 O(nk)
常数阶 O(1)
无论代码执行了多少行,只要是没有循环等复杂结构,那这个代码的时间复杂度就都是 O(1),如:3B
int i = 1;int j = 2;++i;j++;int m = i + j;
线性阶 O(n)
消耗的时间是随着 n 的变化而变化的,因此这类代码都可以用 O(n)来表示它的时间复杂度。
for (i = 0; i <= n; ++i) {j = i;j++;}
对数阶 O(logN)
如果 ax =N(a>0,且 a≠1),那么数 x 叫做以 a 为底 N 的对数,记作 x=logaN,读作以 a 为底 N 的对数,其中 a 叫做对数的底数,N 叫做真数。 一般地,函数 y=logaX(a>0,且 a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。 其中 x 是自变量,函数的定义域是(0,+∞),即 x>0。它实际上就是指数函数的反函数,可表示为 x=ay。因此指数函数里对于 a 的规定,同样适用于对数函数。
int i = 1;while(i<n) {i = i * 2;}
平方阶 O(n2)
平方阶 O(n2) 就更容易理解了,如果把 O(n) 的代码再嵌套循环一遍,它的时间复杂度就是 O(n2) 了。
数据结构
数据结构的存储方式只有两种:数组(顺序存储)和链表(链式存储)。
数组由于是紧凑连续存储,可以随机访问,通过索引快速找到对应元素,而且相对节约存储空间。但正因为连续存储,内存空间必须一次性分配够,所以说数组如果要扩容,需要重新分配一块更大的空间,再把数据全部复制过去,时间复杂度 O(N);而且你如果想在数组中间进行插入和删除,每次必须搬移后面的所有数据以保持连续,时间复杂度 O(N)。
链表因为元素不连续,而是靠指针指向下一个元素的位置,所以不存在数组的扩容问题;如果知道某一元素的前驱和后驱,操作指针即可删除该元素或者插入新元素,时间复杂度 O(1)。但是正因为存储空间不连续,你无法根据一个索引算出对应元素的地址,所以不能随机访问;而且由于每个元素必须存储指向前后元素位置的指针,会消耗相对更多的储存空间。
链表
单向链表
双向链表
循环链表
数组
栈
队列
堆
树
树的遍历方式
- 前序遍历
- 中序遍历
- 后序遍历
图
布隆过滤器
LRU Cache
散列表
并查集
算法
其实算法方面在前端的实际项目中涉及得并不多,但还是需要精通一些基础性的算法,一些公司还是会有这方面的需求和考核,建议大家还是需要稍微准备下,这属于加分题。
排序算法
- 冒泡排序: 两两比较
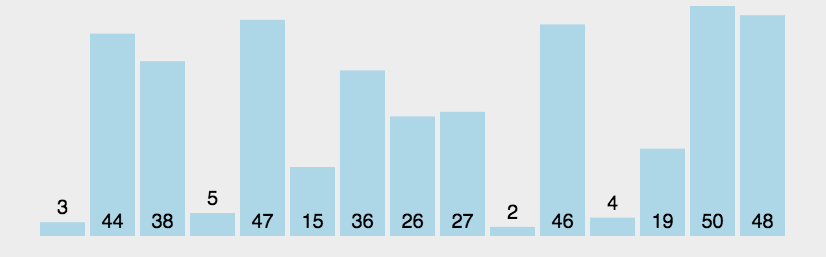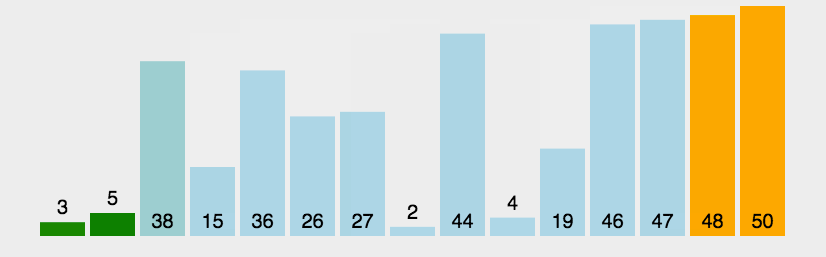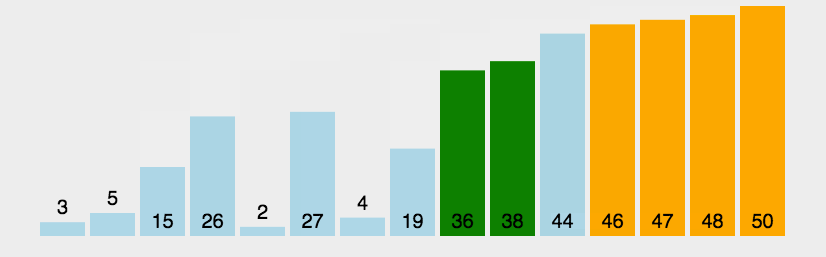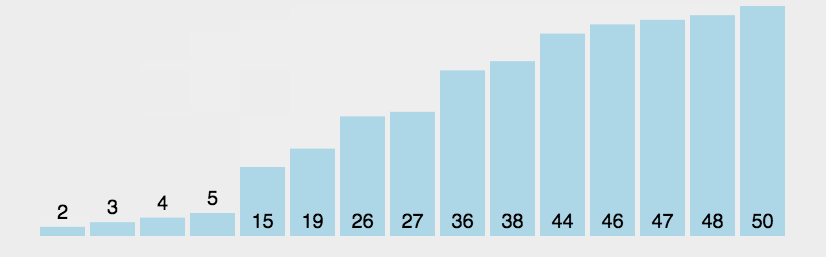
function bubleSort(arr) {var len = arr.length;for (let outer = len; outer >= 2; outer--) {for (let inner = 0; inner <= outer - 1; inner++) {if (arr[inner] > arr[inner + 1]) {[arr[inner], arr[inner + 1]] = [arr[inner + 1], arr[inner]];}}}return arr;}
- 选择排序: 遍历自身以后的元素,最小的元素跟自己调换位置
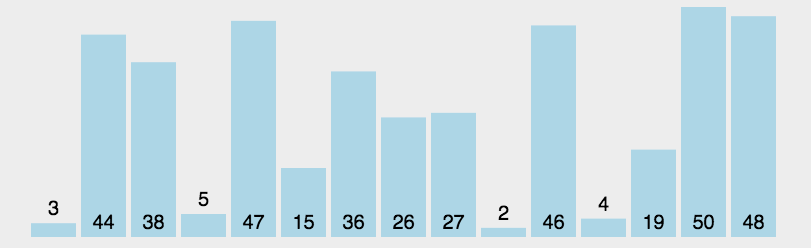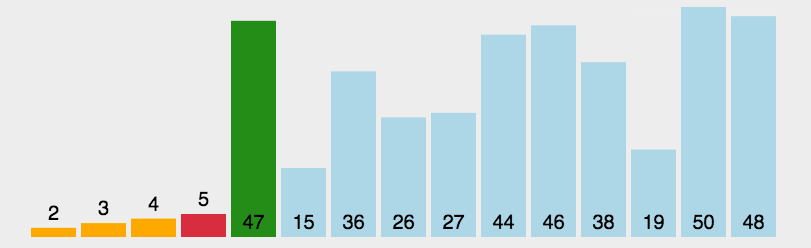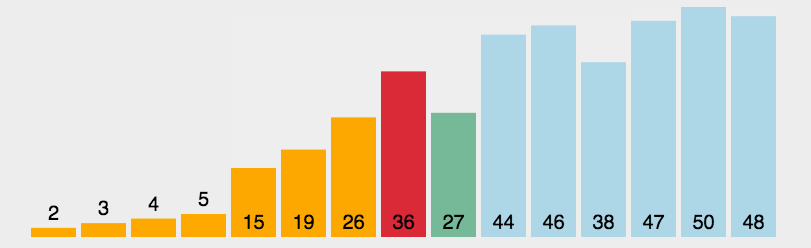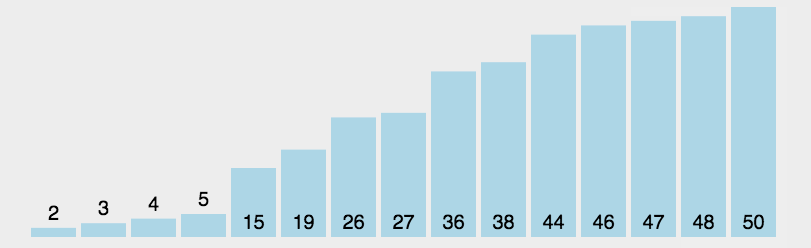
function selectSort(arr) {var len = arr.length;for (let i = 0; i < len - 1; i++) {for (let j = i; j < len; j++) {if (arr[j] < arr[i]) {[arr[i], arr[j]] = [arr[j], arr[i]];}}}return arr;}
- 插入排序: 即将元素插入到已排序好的数组中

function insertSort(arr) {for (let i = 1; i < arr.length; i++) {//外循环从1开始,默认arr[0]是有序段for (let j = i; j > 0; j--) {//j = i,将arr[j]依次插入有序段中if (arr[j] < arr[j - 1]) {[arr[j], arr[j - 1]] = [arr[j - 1], arr[j]];} else {break;}}}return arr;}
- 快速排序 - 选择基准值(base),原数组长度减一(基准值),使用 splice - 循环原数组,小的放左边(left 数组),大的放右边(right 数组); - concat(left, base, right) - 递归继续排序 left 与 right
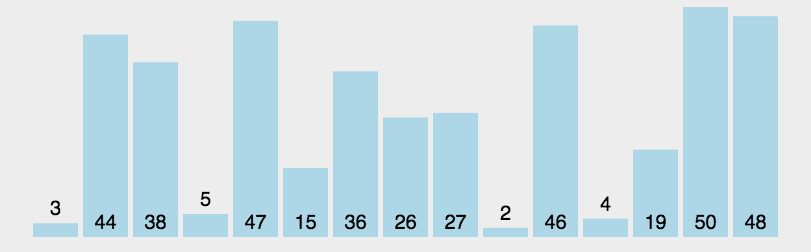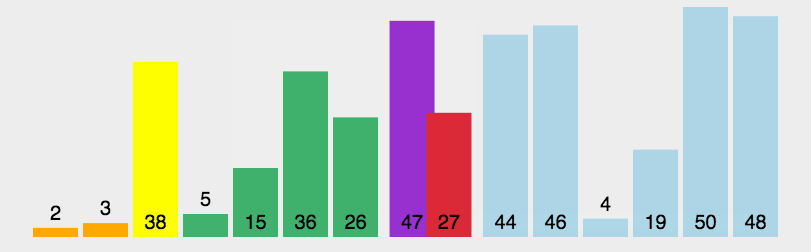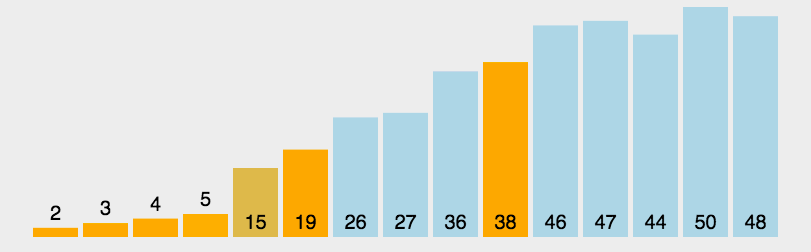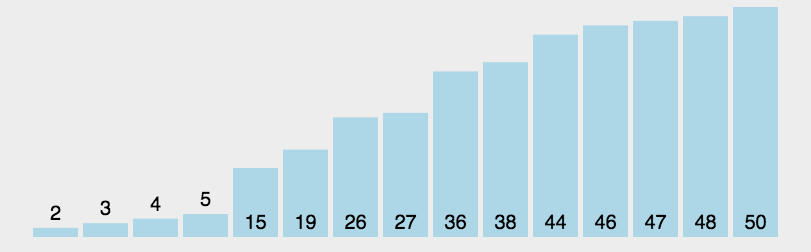
function quickSort(arr) {if (arr.length <= 1) {return arr; //递归出口}var left = [],right = [],current = arr.splice(0, 1);for (let i = 0; i < arr.length; i++) {if (arr[i] < current) {left.push(arr[i]); //放在左边} else {right.push(arr[i]); //放在右边}}return quickSort(left).concat(current, quickSort(right));}
希尔排序:不定步数的插入排序,插入排序
口诀: 插冒归基稳定,快选堆希不稳定

稳定性: 同大小情况下是否可能会被交换位置, 虚拟 dom 的 diff,不稳定性会导致重新渲染;
递归
初始在第一级,到第一级有 1 种方法(s(1) = 1),到第二级也只有一种方法(s(2) = 1), 第三级(s(3) = s(1) + s(2))
function cStairs(n) {if (n === 1 || n === 2) {return 1;} else {return cStairs(n - 1) + cStairs(n - 2);}}
参考十大经典排序算法
哈希算法
二分查找
搜索算法
字符串算法
1. 五大算法
贪心算法
局部最优解法
分治算法
分成多个小模块,与原问题性质相同
位运算
回溯算法
发现原先选择不优时,退回重新选择
动态规划
每个状态都是过去历史的一个总结
实例
两数之和
数据树
- 二叉树: 最多只有两个子节点 - 完全二叉树 - 满二叉树 - 深度为 h, 有 n 个节点,且满足 n = 2^h - 1
- 二叉查找树: 是一种特殊的二叉树,能有效地提高查找效率 - 小值在左,大值在右 - 节点 n 的所有左子树值小于 n,所有右子树值大于 n
 - 遍历节点 - 前序遍历 - 1. 根节点 - 2. 访问左子节点,回到 1 - 3. 访问右子节点,回到 1 - 中序遍历 - 1. 先访问到最左的子节点 - 2. 访问该节点的父节点 - 3. 访问该父节点的右子节点, 回到 1 - 后序遍历 - 1. 先访问到最左的子节点 - 2. 访问相邻的右节点 - 3. 访问父节点, 回到 1 - 插入与删除节点
- 遍历节点 - 前序遍历 - 1. 根节点 - 2. 访问左子节点,回到 1 - 3. 访问右子节点,回到 1 - 中序遍历 - 1. 先访问到最左的子节点 - 2. 访问该节点的父节点 - 3. 访问该父节点的右子节点, 回到 1 - 后序遍历 - 1. 先访问到最左的子节点 - 2. 访问相邻的右节点 - 3. 访问父节点, 回到 1 - 插入与删除节点天平找次品
有 n 个硬币,其中 1 个为假币,假币重量较轻,你有一把天平,请问,至少需要称多少次能保证一定找到假币?
三等分算法:
- 将硬币分成 3 组,随便取其中两组天平称量
- 平衡,假币在未上称的一组,取其回到 1 继续循环
- 不平衡,假币在天平上较轻的一组, 取其回到 1 继续循环
TopK 问题
如从海量数字中寻找最大的 k 个,这类问题我们称为 TOPK 问题,通常使用堆来解决:
- 求前 k 大,用最小堆
- 求前 k 小,用最大堆